
 |
| ||
|
|
 |
Этот Документ | ||||
 | |||||
 |
SummaryPlus |  |
|||
 |
Полный Текст + Ссылки |  |
|||
 |
Изображения ·Thumbnail |  |
|||
 |
PDF (448 K) |  |
|||
 | |||||
 |
Действия | ||||
 | |||||
 |
Процитированный | ||||
 |
Сохраните как Предупреждение Цитаты | ||||
 |
Почтовая Статья | ||||
 |
Экспортная Цитата | ||||
 |
|||||
Здравая основанная на позиции маршрутизация для беспроводных специальных сетей
Kousha Moaveninejad
 , Песня Жировика-Zhan
, Песня Жировика-Zhan  и Литий Сянцзяна-яна
и Литий Сянцзяна-яна 
Отдел Информатики, Институт Иллинойса Технологии, Чикаго, Иллинойс 60616, Соединенные Штаты
Доступный онлайн 15 сентября 2004.
Мы считаем беспроводную специальную сеть составленной из ряда беспроводных узлов распределенный в двух размерных самолетах. Несколько протоколов маршрутизации, основанных на позициях мобильных хостов, были предложены в литературе. Типичное предположение в этих протоколах - то, что всем беспроводным узлам смоделировал однородные области передачи диск модуля, сосредоточенный в каждом беспроводном узле. Однако, все эти протоколы, вероятно, потерпят неудачу, если диапазоны передачи мобильных хостов изменятся из-за естественных или искусственных препятствий или погодных условий. Эти протоколы могут потерпеть неудачу, потому что или некоторые подключения, которые используются, направляя протоколы, не существуют, который эффективно приводит к разъединению сети, или использование некоторых подключений вызывает livelocks. В этой газете мы описываем здравый протокол маршрутизации, который терпит примерно до 40 % изменения в диапазонах передачи мобильных хостов. Более точно, наш протокол гарантирует поставку сообщения в связанной специальной сети всякий раз, когда отношение максимального диапазона передачи к минимальному диапазону передачи самое большее![]() .
.
Ключевые слова: Ограниченная маршрутизация; структура Planar; Беспроводные специальные сети ![]()
Последние годы видели большое количество исследования в беспроводных сетях, особенно специальных беспроводных сетях из-за его потенциальных приложений в различных ситуациях, таких как поле битвы, чрезвычайное облегчение, и так далее. Один из ключевых вызовов в дизайне специальных сетей - развитие динамических протоколов маршрутизации, которые могут эффективно найти маршруты между двумя узлами коммуникации. В последние годы, множество маршрутизации протоколов [6], [16], [17], [18], [19] и [22] предназначенный определенно для специальной окружающей среды было развито. Предложенные протоколы маршрутизации могут быть категоризированы как управляемые таблицей протоколы или управляемые запросами протоколы. Управляемые таблицей протоколы маршрутизации поддерживают современную информацию маршрутизации между каждой парой узлов. Изменения к топологии поддержаны, размножая обновления топологии всюду по сети. Начатый источником По требованию Маршрутизация создает маршруты только когда желательно исходным узлом. В это время процесс открытия маршрута начат в пределах сети. Для обзора государства искусства маршрутизации протоколов, см. обзоры Royer и Toh [21] и Ramanathan и Steenstrup [20]. Открытие маршрута может быть очень дорогим в затратах связи, уменьшая время ответа сети. С другой стороны явное обслуживание маршрута может быть еще более дорогостоящим в явной коммуникации существенной информации маршрутизации.
Недавно, много исследователей предложили использование информации местоположения, чтобы уменьшить количество трафика управления. Ko и Vaidya [10] по существу используют протокол DSR, но предполагают, что узел вперед пакет к узлу, только если это находится в зоне запроса, которая, вероятно, будет содержать путь желательному адресату. Протокол [2] МЕЧТЫ использует ограниченное наводнение пакетов данных. С другой стороны, другой набор жадно-на основе протоколов маршрутизации, которые полностью избегают парадигмы наводнения и каждого узла, выбирает следующий узел, чтобы отправить пакеты, основанные на информации в заголовке пакета, и позиции его местных соседей, были предложены недавно. Этот сосед отобран, в местном масштабе оптимизируя некоторые критерии, такие как длина пути адресату, или различие руководства между адресатом и соседом.
Позвольте s быть исходным узлом, t быть узлом адресата, и u быть текущим узлом u, который имеет пакет и решит который узел отправить пакеты. В Компасе, Направляющем [11], узел u находит следующий узел реле v таким образом, что угол 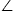 vut является наименьшим среди всех соседей u в данной топологии. Изменение под названием Случайная Маршрутизация Компаса также предложено в [11]. В Жадной Маршрутизации [4], узел u находит следующий узел реле v таким образом, что расстояние
vut является наименьшим среди всех соседей u в данной топологии. Изменение под названием Случайная Маршрутизация Компаса также предложено в [11]. В Жадной Маршрутизации [4], узел u находит следующий узел реле v таким образом, что расстояние  vt
vt является наименьшим среди всех соседей u в данной топологии. В Большинстве Отправления, Направляющего [23], узел u находит следующий узел реле v таким образом, что
является наименьшим среди всех соседей u в данной топологии. В Большинстве Отправления, Направляющего [23], узел u находит следующий узел реле v таким образом, что  v′t
v′t является наименьшим среди всех соседей u в данной топологии, где v ′ является проектированием v на едином времени сегмента В Самом дальнем Соседе, Направляющем узел u, находит самый дальний узел v как отправление узла среди всех соседей u в данной топологии таким образом что
является наименьшим среди всех соседей u в данной топологии, где v ′ является проектированием v на едином времени сегмента В Самом дальнем Соседе, Направляющем узел u, находит самый дальний узел v как отправление узла среди всех соседей u в данной топологии таким образом что 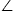 vut
vut 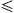 α. Здесь угол α является параметром, который является меньше чем π/2 типично. Другое изменение - Самая близкая Соседняя Маршрутизация: узел u находит самый близкий узел v как отправление узла среди всех соседей u в данной топологии таким образом что
α. Здесь угол α является параметром, который является меньше чем π/2 типично. Другое изменение - Самая близкая Соседняя Маршрутизация: узел u находит самый близкий узел v как отправление узла среди всех соседей u в данной топологии таким образом что 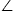 vut
vut 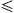 α. Заметьте, что этому показывают в [4] и [11], что маршрутизация компаса, случайная маршрутизация компаса и жадная маршрутизация гарантируют, что освободили пакеты из источника адресату, если триангуляция Delaunay используется как сетевая топология. Здесь сетевой Г топологии по набору, V из беспроводных узлов - триангуляция Delaunay, если circumcircle каждого треугольника uvw (с ультрафиолетовым, подводным, wv в G) не содержит узла от V внутренней части. Однако, дорого создать триангуляцию Delaunay в распределенной манере. Очевидно, есть несколько сценариев, в которых терпит неудачу жадная маршрутизация, если триангуляция Delaunay не используется. Мы предложили структуру, названную местной триангуляцией Delaunay [15], чтобы приблизить триангуляцию Delaunay. Доказательство, что они ограничивали протоколы маршрутизации, гарантирующие поставку, не держится больше в этой местной триангуляции Delaunay, хотя в большинстве случаев, эти жадные протоколы маршрутизации действительно воздействуют на местную триангуляцию Delaunay.
α. Заметьте, что этому показывают в [4] и [11], что маршрутизация компаса, случайная маршрутизация компаса и жадная маршрутизация гарантируют, что освободили пакеты из источника адресату, если триангуляция Delaunay используется как сетевая топология. Здесь сетевой Г топологии по набору, V из беспроводных узлов - триангуляция Delaunay, если circumcircle каждого треугольника uvw (с ультрафиолетовым, подводным, wv в G) не содержит узла от V внутренней части. Однако, дорого создать триангуляцию Delaunay в распределенной манере. Очевидно, есть несколько сценариев, в которых терпит неудачу жадная маршрутизация, если триангуляция Delaunay не используется. Мы предложили структуру, названную местной триангуляцией Delaunay [15], чтобы приблизить триангуляцию Delaunay. Доказательство, что они ограничивали протоколы маршрутизации, гарантирующие поставку, не держится больше в этой местной триангуляции Delaunay, хотя в большинстве случаев, эти жадные протоколы маршрутизации действительно воздействуют на местную триангуляцию Delaunay.
Чтобы преодолеть отказ всех этих жадно-на основе стратегий маршрутизации, несколько исследователей предложили другой набор ограниченных протоколов маршрутизации, которые в основном используют правое правило гарантировать поставку пакетов. Плоская сетевая топология, которая может быть создана эффективно в распределенной манере, требуется для успеха всех ограниченный протокол маршрутизации. Lin и др. [23] предложила первый ограниченный алгоритм, который гарантирует поставку, запоминая прошлый трафик в узлах. Bose и др. [4] предложил использовать граф Габриэля как основную структуру для Лица, направляющего метод. Впоследствии, Karp и др. [7] обсуждаемый подробно среднего уровня доступа и проводимых экспериментов с двигающимися узлами для Лица, направляющего метод. Barriére и др. [1] расширял схему на графах, которые являются нечеткими графами модуля, то есть, два узла связаны, если их расстояние в большинстве r, не связанном, если расстояние по крайней мере R, и может быть связано иначе. Они показывали тем своим работам алгоритма правильно если![]() . Маршрутизация согласно правому правилу, которое гарантирует поставку в плоских графах [3], также используется, когда простая жадно-на основе эвристика маршрутизации терпит неудачу.
. Маршрутизация согласно правому правилу, которое гарантирует поставку в плоских графах [3], также используется, когда простая жадно-на основе эвристика маршрутизации терпит неудачу.
Все предыдущие методы (кроме [1]) предполагали, что у всех беспроводных узлов есть тот же самый диапазон передачи, и узел u может получить сообщение от другого узла v, пока расстояние между ними - меньше чем однородный глобальный диапазон передачи. Следовательно, все беспроводные узлы V вместе определяют граф диска модуля UDG (V), у которого есть ультрафиолетовый край, если и только если Евклидово расстояние,  ультрафиолетовое
ультрафиолетовое между u и v, является меньше чем одним модулем. Несколько плоских структур (таких как RNG, СТРОИТЕЛЬНОЕ СТЕКЛО) были предложены, чтобы использоваться как основная сетевая топология UDG для ограниченных протоколов маршрутизации, которые гарантируют поставку пакетов.
между u и v, является меньше чем одним модулем. Несколько плоских структур (таких как RNG, СТРОИТЕЛЬНОЕ СТЕКЛО) были предложены, чтобы использоваться как основная сетевая топология UDG для ограниченных протоколов маршрутизации, которые гарантируют поставку пакетов.
Однако, графы, представляющие ссылки коммуникации, редко так полностью определяются как графы диска модуля. Мы таким образом считаем общую структуру произвольных графов определенной пунктами в самолете, геометрических графах. Например, для радиосвязей, у различных узлов может быть различный радиус передачи. Следовательно, два узла могут общаться непосредственно, если они в пределах диапазона передачи друг друга, то есть, между этими двумя узлами есть ссылка коммуникации. Граф, сформированный всеми такими ссылками коммуникации, отличается от традиционного дискового графа, в котором два узла связаны прямым краем, если два соответствующих диска, сосредоточенные в этих двух узлах, пересекаются. И для радиосвязей, два узла иногда не могут общаться непосредственно даже при том, что они в пределах диапазона передачи друг друга, из-за блокирования сигнала некоторым барьером. После этого, мы называем граф, сформированный всеми беспроводными узлами и краями ультрафиолетовое представление, которое два узла u и v могут сообщить непосредственно, граф коммуникации. Позвольте рутению быть диапазоном передачи узла u. Граф коммуникации тогда называют взаимным графом коммуникации (МГ), когда есть край ультрафиолетовая iff  ультрафиолетовая
ультрафиолетовая
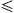 минута {рутений, rv}.
минута {рутений, rv}.
Это просто создать конфигурацию ряда узлов (их позиции и диапазоны передачи) таким образом, что нет никакого плоского подграфа оригинального графа коммуникации, когда у узлов есть различные диапазоны передачи, и некоторые ссылки могут отсутствовать из-за блокирования сигнала. Мы таким образом должны положиться на некоторые виртуальные ссылки, чтобы построить плоскую структуру. Это - природа, чтобы просить, чтобы мы использовали как меньше виртуальных ссылок насколько возможно.
В этой газете мы представляем новую методику построения плоской топологии для графов коммуникации, который не является UDG. Наши моделирования показывают существенному усовершенствованию сообщений, используемых нашим методом по сравнению с предыдущим методом без lossing работа маршрутизации.
Остальная часть бумаги организована следующим образом. В Разделе 2, мы обсуждаем подробно сетевой модели, используемой в этой газете, и рассматриваем некоторые предыдущие результаты на здравой основанной на позиции маршрутизации для этой модели. Мы представляем свою методику в Разделе 3. В Разделе 4, мы изучаем работу нашего метода по сравнению с предыдущим методом. Мы заключаем свою бумагу в Разделе 5.
Мы считаем беспроводную специальную сеть (или сеть датчика) со всеми узлами распределенными в двумерном самолете. Предположите, что у всех беспроводных узлов есть отличительные тождества, и каждый статический беспроводный узел знает свою позицию information1 или через малую мощность Глобальная Система Позиции (GPS) получатель или через некоторый другой путь. Передающим по радио одним перелетом каждый узел u может послать свою информацию местоположения во все узлы в пределах области передачи u. Всюду по этой бумаге радиопередача узлом u означает, что u посылает сообщение во все узлы в пределах его области передачи.
В беспроводных специальных сетях область передачи узла u определена как местоположения, где радио-сигнал, отосланный узлом u, может быть признан узлом получателя. Для простоты традиционно предполагается, что область передачи каждого беспроводного узла - диск с радиусом модуля. Здесь диск сосредоточился в узле u с рутением радиуса, обозначенным D (u, рутением), набор пунктов, расстояние которых к u в большинстве рутения. Таким образом все узлы вместе определяют граф диска модуля как граф коммуникации. Однако, графы, представляющие ссылки коммуникации, редко так полностью определяются как граф диска модуля. У различных узлов может быть различный радиус передачи, и что еще более важно область передачи узла никогда не столь же прекрасна как диск. Рассматривая эту несовершенную область передачи, предыдущие алгоритмы маршрутизации, которые гарантируют поставку пакета, используя некоторый плоский подграф как сетевая топология, вероятно, потерпят неудачу, так как трудность построения плоского подграфа от графа коммуникации и некоторых ссылок может отсутствовать. В худшем случае граф коммуникации мог быть очень сложным. Чтобы иметь некоторое значащее исследование, мы предполагаем, что у каждого узла u есть максимальный Рутений радиуса передачи и минимальный рутений радиуса передачи. Эти два порога зависят и от окружающей среды и от технологии мобильных хостов. Таким образом, область передачи узла u (область, где узлы могут получить передачу u) содержится в диске D (u, Рутений) и содержит диск D (u, рутений). См. рис. 1 для иллюстрации. Таким образом, два мобильных хоста u и v не могут общаться непосредственно (то есть, обменные сообщения), если их Евклидово расстояние превышает минуту значения (Рутений, Rv). Наоборот, два мобильных хоста всегда взаимно достижимы, если их Евклидово расстояние ниже минуты значения (рутений, rv).
Рис. 1. Область передачи узла смоделирована квазидиском.
Сеть тогда представлена геометрическим ненаправленным графом, Г = (V, E), с вершинами, представляющими мобильные хосты, и края, представляющие ссылки коммуникации. Набор вершин V является таким образом рядом пунктов в Евклидовом самолете. Позвольте  ультрафиолетовый
ультрафиолетовый быть Евклидовом расстоянием между пунктами u и v в самолете. Набор краев E удовлетворяет {uv
быть Евклидовом расстоянием между пунктами u и v в самолете. Набор краев E удовлетворяет {uv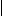 u, v
u, v 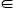 V,
V,  ультрафиолетовая
ультрафиолетовая
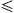 минута {рутений, rv}}
минута {рутений, rv}} 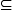 E и E
E и E 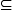 {uv
{uv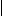 u, v
u, v 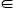 V,
V,  ультрафиолетовая
ультрафиолетовая
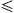 минута {Рутений, Rv}}. Узлы, соответствующие мобильным хостам, и краям между мобильным хостом и его соседями, формируют Г графа. Два мобильных хоста u и v с минутой {рутений, rv}
минута {Рутений, Rv}}. Узлы, соответствующие мобильным хостам, и краям между мобильным хостом и его соседями, формируют Г графа. Два мобильных хоста u и v с минутой {рутений, rv} 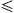
 ультрафиолетовая
ультрафиолетовая
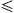 минута {Рутений, Rv} может или, возможно, не в состоянии общаться непосредственно.
минута {Рутений, Rv} может или, возможно, не в состоянии общаться непосредственно.
Более точно, позвольте R (u) быть областью передачи узла u, то есть, от того, где другие узлы могут получить сигнал, посланный u. Тогда наше предположение - то, что R (u) содержится в диске D (u, Рутений) и содержит диск D (u, рутений). Два узла u и v могут общаться непосредственно iff, они в области передачи друг друга. Позвольте мне (u) быть всеми узлами, которые могут послать сигнал в u, то есть, я (u) = {v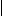 u
u 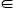 R (v)}. Позвольте T (u) быть всеми узлами, которые могут получить сигнал от u, то есть, T (u) = {v
R (v)}. Позвольте T (u) быть всеми узлами, которые могут получить сигнал от u, то есть, T (u) = {v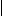 v
v 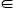 R (u)}. Позвольте N (u) быть соседями u в Г, то есть, N (u) = я (u) ∩ T (u).
R (u)}. Позвольте N (u) быть соседями u в Г, то есть, N (u) = я (u) ∩ T (u).
Мы отмечаем, что условия передачи не изменяются быстро со временем, по сравнению со скоростью электронной связи. Это подразумевает, что сеть может измениться, например, из-за изменения в погодных условиях, но именно в масштабе времени позволяет простой сброс сети. Таким образом, мы предполагаем с этого времени, что подключения между мобильными хостами установлены. Однако, структура этих подключений не известна, и это - роль нашего протокола, чтобы гарантировать поставку сообщения в этой неизвестной сети.
Моделирование области передачи квазидиском не является нашим новшеством: Barriŕre и др. [1] также применил эту модель. Они предполагали, кроме того, что Рутений радиуса - то же самое (скажите, что у всех узлов есть значение R) для всех узлов u, и у рутения есть то же самое значение r. Они дали протокол с тремя фазами, который гарантирует поставку пакета пока![]() . Центральная часть их протокола - конструкция плоской структуры в распределенной манере. Начиная с оригинала общаются, граф, возможно, не содержит плоский подграф вообще, это использует некоторые виртуальные ссылки. Чтобы отличить созданные виртуальные ссылки от других, мы называем ссылки коммуникации в оригинальном графе как фактические ссылки. Это определяет виртуальные ссылки, используя рекурсивный подход: учитывая любую ультрафиолетовую ссылку (могло быть виртуальным или фактическим), если есть узел w в дисковом диске (u, v), то добавляют подводные ссылки и vw к виртуальным ссылкам, если они не фактические ссылки. Это просто показать этому, у всех виртуальных ссылок есть длина в большинстве R индукцией. С тех пор
. Центральная часть их протокола - конструкция плоской структуры в распределенной манере. Начиная с оригинала общаются, граф, возможно, не содержит плоский подграф вообще, это использует некоторые виртуальные ссылки. Чтобы отличить созданные виртуальные ссылки от других, мы называем ссылки коммуникации в оригинальном графе как фактические ссылки. Это определяет виртуальные ссылки, используя рекурсивный подход: учитывая любую ультрафиолетовую ссылку (могло быть виртуальным или фактическим), если есть узел w в дисковом диске (u, v), то добавляют подводные ссылки и vw к виртуальным ссылкам, если они не фактические ссылки. Это просто показать этому, у всех виртуальных ссылок есть длина в большинстве R индукцией. С тех пор![]() , очевидно, у одной из ссылок подводных и vw должна быть длина самое большее
, очевидно, у одной из ссылок подводных и vw должна быть длина самое большее![]() , то есть, это - фактическая ссылка в графе коммуникации. После сбора всех виртуальных ссылок алгоритм тогда применяет структуру Gabriel к новому графу (со всеми фактическими ссылками и виртуальными ссылками). Простое доказательство может показать этому, заключительная структура - связанный плоский граф.
, то есть, это - фактическая ссылка в графе коммуникации. После сбора всех виртуальных ссылок алгоритм тогда применяет структуру Gabriel к новому графу (со всеми фактическими ссылками и виртуальными ссылками). Простое доказательство может показать этому, заключительная структура - связанный плоский граф.
Однако, хотя виртуальные ссылки необходимы для того, чтобы создать плоскую структуру, их протокол создает много ненужных виртуальных ссылок. Они также дали пример, который показывает этому, это создает много таких ненужных виртуальных ссылок, даже оригинальный граф коммуникации уже - плоский рис. 2 структуры 2, иллюстрирует такой пример. Есть 2n узлы: n узлы u1, u2, …, un одинаково распределены на левом сегменте; n узлы v1, v2, …, vn одинаково распределены на правильном сегменте. Они размещены таким образом что 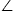 uiui+1vi = π/2,
uiui+1vi = π/2, 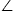 uivi+1vi = π/2, в дополнение к u1v1 = R и unvn = r +
uivi+1vi = π/2, в дополнение к u1v1 = R и unvn = r +  для произвольно маленького положительного действительного числа
для произвольно маленького положительного действительного числа . Простое выполнение их показов протокола, что у заключительной плоской структуры есть все ссылки uiui+1, vivi+1, (1
. Простое выполнение их показов протокола, что у заключительной плоской структуры есть все ссылки uiui+1, vivi+1, (1 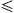 я
я 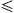 n − 1) и unvn (но никакая ссылка u1v1). Заметьте, что у оригинального графа коммуникации есть ссылка u1v1 вместо виртуальной ссылки unvn. У самого короткого пути, соединяющегося u1 и v1 в этой заключительной плоской структуре, есть длина
n − 1) и unvn (но никакая ссылка u1v1). Заметьте, что у оригинального графа коммуникации есть ссылка u1v1 вместо виртуальной ссылки unvn. У самого короткого пути, соединяющегося u1 и v1 в этой заключительной плоской структуре, есть длина![]() . Есть O (n) ненужные виртуальные ссылки uivi + 1 и ui + 1vi созданный. Заметьте, что оригинальный граф коммуникации уже - плоская структура.
. Есть O (n) ненужные виртуальные ссылки uivi + 1 и ui + 1vi созданный. Заметьте, что оригинальный граф коммуникации уже - плоская структура.
Рис. 2. Чрезмерные виртуальные ссылки созданы (тогда удаленный в левом случае).
Если мы позволим узлам ui и ui + 1 (так сделайте vi и vi + 1), произвольно закройтесь, то их протокол добавит все края uivj как виртуальные ссылки. Таким образом, в худшем случае, это могло добавить O (n2) ненужные виртуальные ссылки и затем удалить все эти виртуальные ссылки (кроме unvn), даже оригинальный граф коммуникации является плоским. Правильное число показов рис. 2, что их метод добавляет O (n) виртуальные ссылки к заключительной структуре даже, это является ненужным. В этой газете мы представляем новую методику, чтобы создать плоскую структуру, которая более эффективна в терминах связи и власти, охватывающей отношение, не создавая чрезмерные виртуальные ссылки.
Прежде, чем мы обсудим свой метод, мы сначала рассматриваем некоторые определения, которые будут использоваться позже. Для любой пары узлов u и v, позвольте lune (u, v) быть пересечением двух дисков, сосредоточенных в u и v с  ультрафиолетовым радиусом
ультрафиолетовым радиусом 
 и диска (u, v) быть диском с ультрафиолетовым диаметром. Позвольте диску (u, v, w) быть circumcircle треугольника
и диска (u, v) быть диском с ультрафиолетовым диаметром. Позвольте диску (u, v, w) быть circumcircle треугольника 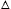 uvw. Относительный граф соседства [24], обозначенный RNG (V), состоит из всех краев, ультрафиолетовых таким образом, что lune (u, v) пуст от других узлов внутри. Граф Габриэля [5] СТРОИТЕЛЬНОЕ СТЕКЛО (V) содержит все края, ультрафиолетовые таким образом, что диск (u, v) пуст от других узлов. Предположите, что никакие четыре вершины V не являются cо-проспектом. Триангуляция Delaunay, обозначенная Del (V), является союзом всех треугольников
uvw. Относительный граф соседства [24], обозначенный RNG (V), состоит из всех краев, ультрафиолетовых таким образом, что lune (u, v) пуст от других узлов внутри. Граф Габриэля [5] СТРОИТЕЛЬНОЕ СТЕКЛО (V) содержит все края, ультрафиолетовые таким образом, что диск (u, v) пуст от других узлов. Предположите, что никакие четыре вершины V не являются cо-проспектом. Триангуляция Delaunay, обозначенная Del (V), является союзом всех треугольников 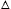 uvw таким образом, что диск (u, v, w) пуст от других узлов. Очевидно, RNG (V) СТРОИТЕЛЬНОЕ СТЕКЛО
uvw таким образом, что диск (u, v, w) пуст от других узлов. Очевидно, RNG (V) СТРОИТЕЛЬНОЕ СТЕКЛО 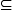 (V) D
(V) D 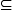 el (V). Недавно, мы [15] также определяем последовательность названной структуры, ограничивал Delaunay. Треугольник
el (V). Недавно, мы [15] также определяем последовательность названной структуры, ограничивал Delaunay. Треугольник 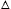 uvw в UDG называют k-localized Delaunay треугольником, если диск (u, v, w) не содержит вершины, которая является в пределах перелетов k u, v, или w. k-localized Delaunay граф у более чем V, обозначенных LDel (k) (V), есть точно все края Габриэля в UDG и края всего k-localized Delaunay треугольники.
uvw в UDG называют k-localized Delaunay треугольником, если диск (u, v, w) не содержит вершины, которая является в пределах перелетов k u, v, или w. k-localized Delaunay граф у более чем V, обозначенных LDel (k) (V), есть точно все края Габриэля в UDG и края всего k-localized Delaunay треугольники.
В этой газете мы будем использовать сетевую модель, используемую Barriŕre и др. [1], то есть, все узлы имеют тот же самый Рутений радиуса, говорят R, и все узлы имеют тот же самый рутений, говорят r, и![]() .
.
Наша схема маршрутизации состоит из пяти фаз: Ссылка, Собирающая фазу, фазу Габриэля, Виртуальная ссылка, Добавляющая фазу, фазу Извлечения, и фазу Маршрутизации. В Ссылке, Собирающей фазу, каждый узел u соберет все фактические ультрафиолетовые ссылки, то есть, u, и v может общаться взаимно и непосредственно. Цель фазы Габриэля состоит в том, чтобы удалить некоторые края так число пересечений, обработанных в Виртуальной ссылке, Добавляющей уменьшения фазы, цель Виртуальной ссылки, Добавляющей, что фаза должна добавить некоторые края (названный виртуальными краями) к физическому графу коммуникации, чтобы гарантировать обеспечение связи графа после того, как фаза Извлечения выполнена. Другими словами фаза Извлечения могла бы разъединить граф, если мы не добавляем виртуальные края. Цель фазы извлечения состоит в том, чтобы удалить пересечения из физического графа коммуникации и произвести плоский граф. Как только фаза извлечения сделана, фаза маршрутизации выполняет поставку сообщения между мобильными хостами. Все вычисления во всех фазах являются местными и не требуют никакого центрального контроллера.
Фаза Габриэля и Виртуальная ссылка, Добавляющая фазу, являются новыми вкладами, и будут описаны подробно. Фаза маршрутизации - в основном то же самое как фаза маршрутизации в [4] и [7], и чередует жадную маршрутизацию с маршрутизацией периметра, то есть, направляя вокруг лиц плоского графа, используя правое правило. Таким образом мы включаем только краткое обсуждение фазы маршрутизации.
Следующие структуры данных и сообщения используются нашим методом:
(1) Структуры Данных:
(a) N (u) = (bDeleted, bActual, bProcessed, (v, vx, vy), (w, wx, wy)): история/финал (фактический или виртуальный) граничит со списком u, где v когда-либо, или теперь сосед u и w - узел реле, если ультрафиолетовая ссылка виртуальна; bDeleted - флажок, чтобы показать, удалялся ли он когда-либо или нет; bActual - флажок, чтобы показать, является ли это фактическим краем или виртуальным краем; bProcessed - флажок, чтобы показать, обрабатывался ли он когда-либо или нет. Первоначально, все флажки Ложны. Если сосед - фактический сосед тогда последний параметр, который является логином и координатой узла реле, не имел бы никакого значения.
(b) L (u) = (bDeleted, bProcessed, (v, vx, vy), (w, wx, wy)): набор всех известных краев vw u, где ни v, ни w не u. Здесь bDeleted - флажок, чтобы показать, удалялся ли он когда-либо или нет; bProcessed - флажок, чтобы показать, обрабатывался ли он когда-либо или нет. Первоначально, все флажки Ложны.
(2) Формат Сообщения:
(a) NewNode (v, vx, vy): узел использует это сообщение, чтобы сообщить другому узлу информация узла v. Здесь (vx, vy) координата узла v.
(b) Подтвердите (u, v): узел u подтверждает узел v, что u может получить сигнал от v.
(c) NewLink (u, v, (ux, uy), (vx, vy)): узел использует это сообщение, чтобы сообщить другому узлу существование ультрафиолетовой ссылки. Здесь ультрафиолетовый могла быть фактическая ссылка или виртуальная ссылка.
(d) CreateLink (u, v, (ux, uy), (vx, vy)): узел использует это сообщение, чтобы сообщить или узлу u или узлу v, чтобы создать виртуальную ультрафиолетовую ссылку.
Прежде, чем мы запустим Габриэля Phase, мы должны создать граф FUDG, таким образом каждый узел будет знать о своих соседях, следующим образом. Первоначально, каждый мобильный хост передает по радио свою собственную позицию геометрии к мобильным хостам в пределах его области передачи. В отличие от модели графа диска модуля, зная позицию геометрии другого мобильного хоста v, мобильный хост u не может определить, может ли это общаться непосредственно с мобильным хостом v. Это только знает, что это может получить сообщение от v, но не уверено, может ли v получить его сигнал. Таким образом, узел u должен послать сообщение, Подтверждают, чтобы подтвердить, что он может получить сообщение от v.
1. Первоначально, каждый узел u устанавливает пустой соседний список N (u) и пустой список L ссылки (u). Каждый узел u передает по радио свою информацию местоположения, посылая сообщение NewNode (u, ux, uy) ко всем узлам в его области передачи, используя местную модель радиопередачи.
2. Когда узел v получает сообщение NewNode (u, ux, uy) от узла u,
(a) если  ультрафиолетовый
ультрафиолетовый > r тогда узел v подтверждает, что узел u, посылая сообщение Подтверждает ((v, vx, vy), u).
> r тогда узел v подтверждает, что узел u, посылая сообщение Подтверждает ((v, vx, vy), u).
(b) если  ультрафиолетовое
ультрафиолетовое
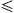 r тогда узел v добавляет отчет (NotDeleted, Фактический, NotProcessed, (u, ux, uy), (пустой указатель, пустой указатель, пустой указатель)) к N (v).
r тогда узел v добавляет отчет (NotDeleted, Фактический, NotProcessed, (u, ux, uy), (пустой указатель, пустой указатель, пустой указатель)) к N (v).
3. Если узел u получает сообщение подтверждения, Подтверждают ((v, vx, vy), u) от узла v, узел u добавляет отчет (NotDeleted, Фактический, NotProcessed, (v, vx, vy), (пустой указатель, пустой указатель, пустой указатель)) к N (u).
Теперь у каждого узла есть информация его соседей с одним перелетом. Это тогда может продолжиться к следующей фазе. Заметьте, что, узел u не должен ждать, чтобы забрать всех его соседей перелета, чтобы запустить фазу Габриэля. Это может выполнить фазу Габриэля всякий раз, когда это получает информацию о новом соседе. Чтобы избежать ненужного перевычисления Габриэля Phase, мы устанавливаем значение TMax блокировки времени, которое является временем, это запустит фазу Габриэля после получения сообщения подтверждения от его первого соседа.
Мы тогда показываем этому, информация ссылки, собранная всеми узлами, последовательна: если у узла u будет ультрафиолетовая ссылка, то у узла v также будет ссылка vu и наоборот. Если  ультрафиолетовое
ультрафиолетовое
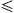 r, то u и v наверняка, которые связываются ультрафиолетовый, существует, и никакое подтверждение не необходимо. Иначе, когда у узла u есть ультрафиолетовая ссылка, он означает, что сообщение запроса, посланное u, получено v, и сообщение подтверждения от v получено u. Следовательно, сообщение запроса от v будет получено u, и сообщение подтверждения u будет получено v. Таким образом, узел v также создаст фактическую ссылку vu.
r, то u и v наверняка, которые связываются ультрафиолетовый, существует, и никакое подтверждение не необходимо. Иначе, когда у узла u есть ультрафиолетовая ссылка, он означает, что сообщение запроса, посланное u, получено v, и сообщение подтверждения от v получено u. Следовательно, сообщение запроса от v будет получено u, и сообщение подтверждения u будет получено v. Таким образом, узел v также создаст фактическую ссылку vu.
Цель этой фазы состоит в том, чтобы удалить некоторые ненужные ссылки из графа FUDG. Это выполнено, распаковывая граф Габриэля графа FUDG с небольшой модификацией. Граф диска модуля, определенный на всех узлах, принимая их диапазоны передачи, является r, подграф графа FUDG. Мы используем UDG (FUDG), чтобы обозначить такой граф диска модуля. Габриэль Phase удаляет все края, которые не принадлежат СТРОИТЕЛЬНОМУ СТЕКЛУ (UDG (FUDG)). Другими словами каждый край, ультрафиолетовый с длиной, меньше чем r удалены, если там существует узел w таким образом что 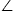 uwv
uwv 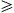 π/2. Удаление ультрафиолетового края выполнено, устанавливая флажок bDeleted узла u, чтобы быть Истинным в списке смежности узла v и наоборот. Эти края будут удалены в Фазе Извлечения, если мы не удалим их перед началами Фазы Извлечения. Мы удаляем их на данном этапе, таким образом у нас будет меньше числа пересечений в Виртуальной ссылке, Добавляющей Фазу.
π/2. Удаление ультрафиолетового края выполнено, устанавливая флажок bDeleted узла u, чтобы быть Истинным в списке смежности узла v и наоборот. Эти края будут удалены в Фазе Извлечения, если мы не удалим их перед началами Фазы Извлечения. Мы удаляем их на данном этапе, таким образом у нас будет меньше числа пересечений в Виртуальной ссылке, Добавляющей Фазу.
Тогда, каждый узел, скажем u, отсылает информацию его соседей, скажем v, флажок bDeleted которого Ложен, посылая сообщение NewLink ((u, ux, uy), (v, vx, vy)). Когда узел, скажем w, который не является ни u, ни v, получает NewLink ((u, ux, uy), (v, vx, vy)), и если (a), ультрафиолетовая ссылка не принадлежит L (w) и (b) или  подводный
подводный
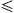 r или
r или  vw
vw
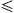 r, то это добавляет отчет (NotDeleted, NotProcessed, (u, ux, uy), (v, vx, vy)) к L (w).
r, то это добавляет отчет (NotDeleted, NotProcessed, (u, ux, uy), (v, vx, vy)) к L (w).
Заметьте, что после фазы Габриэля у нас только есть два набора ссылок (1) подмножество ссылок с длиной в большинстве r, и эти ссылки формируют плоский граф (не обязательно связанный). (2) все фактические ссылки, у которых есть длина, большая чем r, но не больше, чем R (эти ссылки могут пересечь себя или со ссылками от первого подмножества). Наша следующая фаза добавит виртуальные ссылки, таким образом мы сможем удалить пересечения позже.
Рассмотрите любые две пересеченных ссылки xy и ультрафиолетовый. Или этих двух ссылок могла быть виртуальная ссылка или фактическая ссылка. Основной подход нашего метода, чтобы удалить пересечение, не разъединяя сеть основан на следующем наблюдении, иллюстрированном рис. 3. Предположите, что 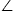 xuy - наибольший угол четырехугольника. Тогда мы можем удалить ссылку xy и добавить икс-единицу ссылки (если это не добавлено прежде) удалить это пересечение и сохранить обеспечение связи. Если добавленная икс-единица ссылки вызывает новые пересечения, мы продолжаем обрабатывать новые пересечения.
xuy - наибольший угол четырехугольника. Тогда мы можем удалить ссылку xy и добавить икс-единицу ссылки (если это не добавлено прежде) удалить это пересечение и сохранить обеспечение связи. Если добавленная икс-единица ссылки вызывает новые пересечения, мы продолжаем обрабатывать новые пересечения.
Рис. 3. Две пересеченных ссылки: каждый будет удален.
Заметьте, что, если мы фактически удаляем ссылку xy из графа немедленно, мы можем закончить тем, что произвели много сообщений из-за следующих явлений: ссылка xy могла быть добавлена назад, когда мы обработаем некоторые другие пересечения, и затем связываемся, xy вызовет новые пересечения снова (хотя мы обработали это прежде). Чтобы избежать этой петли перекрестной обработки, мы только отметим край xy как удалено, но фактически не удалять это из графа теперь. Позже, обрабатывая некоторые другие пересечения, которые вызывают добавление ссылки xy, мы сначала проверяем, существует ли ссылка xy или не (это могло бы быть отмечено как удалено). Если это существует, мы ничего не делаем; иначе, мы добавляем информацию ссылки к узлу x и узлу y.
Так как любая пара узлов с расстоянием в большинстве r может общаться непосредственно, у добавленных виртуальных ссылок есть длина, большая чем r. Мы также доказываем, что у всех введенных виртуальных ссылок есть длина в большинстве R.
Аннотация 1
У всех введенных виртуальных ссылок есть длина в большинстве R.
Доказательство
Мы доказываем это индукцией на времени виртуальной ссылки, введенной структуре. Когда первая виртуальная ссылка введена, у всех ссылок есть длина в большинстве R. Виртуальная ссылка введена, так как есть две предыдущих известных ссылки, пересекают друг друга. Считайте любые две пересеченных ссылки ультрафиолетовыми и xy. См. рис. 3 для иллюстрации. Наибольший угол среди четырех углов поворачивает 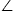 xuy,
xuy, 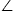 uyv,
uyv, 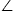 yvx, и
yvx, и 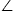 vxu по крайней мере π/2 от руководителя ящика. Предположите, что
vxu по крайней мере π/2 от руководителя ящика. Предположите, что 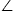 xuy - наибольший угол (связи сломаны в соответствии с наибольшим логином узла вершины). Очевидно, самый короткий край икс-единицы и uy самое большее
xuy - наибольший угол (связи сломаны в соответствии с наибольшим логином узла вершины). Очевидно, самый короткий край икс-единицы и uy самое большее![]() . W.l.o.g., примите это
. W.l.o.g., примите это  uy
uy
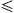
 ux
ux . Следовательно, узел u и y могут получить сообщение друг от друга. Тогда узел u будет знать существование о ссылке xy через узел y, и узел y будет знать существование о ссылке, ультрафиолетовой через узел u. Тогда согласно нашему алгоритму, узел y решит удалить ссылку xy и предлагает добавить икс-единицу ссылок, и uy (фактически uy уже существовал как фактическая ссылка, таким образом только свяжитесь, икс-единица могла быть виртуальной введенной ссылкой). Очевидно, длина, если икс-единица ссылки - меньше чем тот из xy, который является в большинстве R.
. Следовательно, узел u и y могут получить сообщение друг от друга. Тогда узел u будет знать существование о ссылке xy через узел y, и узел y будет знать существование о ссылке, ультрафиолетовой через узел u. Тогда согласно нашему алгоритму, узел y решит удалить ссылку xy и предлагает добавить икс-единицу ссылок, и uy (фактически uy уже существовал как фактическая ссылка, таким образом только свяжитесь, икс-единица могла быть виртуальной введенной ссылкой). Очевидно, длина, если икс-единица ссылки - меньше чем тот из xy, который является в большинстве R.
Когда ссылки xy, или ультрафиолетовый, или оба могли быть виртуальными ссылками, индукцией, виртуальные ссылки, введенные от их пересечения, имеет длину в большинстве R также. Это заканчивает доказательство. 
Мы тогда обсуждаем подробно свой метод добавления виртуальных ссылок. Прежде всего, рассмотрите любые две пересеченных ссылки, скажите ультрафиолетовый и xy, в текущей конфигурации сети. См. рис. 3 для иллюстрации. W.l.o.g., предположите, что 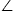 xuy - наибольший угол четырехугольника xuyv (связи сломаны в соответствии с логином вершины). Тогда это просто показать этому или у uy или ux есть длина в большинстве r, то есть, это - фактическая ссылка. Примите это
xuy - наибольший угол четырехугольника xuyv (связи сломаны в соответствии с логином вершины). Тогда это просто показать этому или у uy или ux есть длина в большинстве r, то есть, это - фактическая ссылка. Примите это  uy
uy
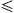 r. Следовательно, и u и y могут обнаружить такое пересечение, так как они знают существование об этих двух ультрафиолетовых ссылках, и xy (узел u знает xy через узел y, и узел y знает ультрафиолетовый через узел u). Чтобы избежать, чтобы они оба обработали это пересечение, мы только позволяем узлу u (с наибольшим углом
r. Следовательно, и u и y могут обнаружить такое пересечение, так как они знают существование об этих двух ультрафиолетовых ссылках, и xy (узел u знает xy через узел y, и узел y знает ультрафиолетовый через узел u). Чтобы избежать, чтобы они оба обработали это пересечение, мы только позволяем узлу u (с наибольшим углом 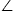 xuy), обрабатывают это. Таким образом, у нас есть следующая процедура добавления виртуальных ссылок.
xuy), обрабатывают это. Таким образом, у нас есть следующая процедура добавления виртуальных ссылок.
1. Предположите, что узел u создает новую ссылку ультрафиолетовый Узел u проверки, хранила ли ссылка ультрафиолетовые пересечения причин с некоторыми ссылками в списке L (u). Если это действительно вызывает пересечение, говорит со ссылкой xy, это идет, чтобы Ступить 3.
2. Предположите, что узел u получает NewLink (u, v, (обман, xy), (yx, yy)) от некоторого соседа. Узел u проверяет, вызывает ли ссылка xy пересечения с некоторыми ссылками, сохраненными в списке N (u). Если это действительно вызывает пересечение, говорит с ультрафиолетовой ссылкой, идет, чтобы Ступить 3.
3. Узел u проверяет, удовлетворены ли следующие условия: (1) 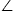 xuy является наибольшим среди четырехугольника xuyv, и (2), ссылка ux не существует. Если условия будут удовлетворены, то узел u добавит, что виртуальная ссылка ux, то есть, добавляет отчет (notDeleted, notProcessed, (x, обман, xy), (y, yx, yy)) к L (u).
xuy является наибольшим среди четырехугольника xuyv, и (2), ссылка ux не существует. Если условия будут удовлетворены, то узел u добавит, что виртуальная ссылка ux, то есть, добавляет отчет (notDeleted, notProcessed, (x, обман, xy), (y, yx, yy)) к L (u).
Заметьте, что узел y может также обнаружить это пересечение. Узел y тогда посылает сообщение в узел x (через реле некоторых других узлов, если ссылка yx виртуальна), то, чтобы просить, чтобы это сформировало виртуальную ссылку ux. Узел y также отмечает ссылку xy удаленный, то есть, установил bDeleted ссылки xy к Истине.
Когда узел x получает сообщение формирования виртуальной икс-единицы ссылки от узла y, узел x добавляет узел u к его списку N (u) и отмечает ссылку xy удаленный также.
Заметьте, что здесь связываются, xy мог быть виртуальной ссылкой также. Коммуникация через ссылку xy будет тогда через реле последовательности фактических ссылок. Кроме того, так как мы проверяем, существует ли ссылка ux или не прежде, чем мы решим добавить эту ссылку, у всех добавленных виртуальных ссылок есть длина по крайней мере r.
Эта фаза очень подобна фазе Габриэля, но с небольшим количеством различий. Края, длина которых больше чем r, могли бы быть удалены, но края, длина которых меньше, чем r не будет удален. Помните, что после фазы Габриэля, у нас только есть два набора краев: (1) края в СТРОИТЕЛЬНОМ СТЕКЛЕ (UDG (FUDG)) формирование плоского графа и с длиной в большинстве r, и (2) все края в оригинальном графе коммуникации с длиной в (r, R]. В виртуальной ссылке, добавляющей фазу, мы только добавляем виртуальные ссылки с длиной, большей чем r. Фаза Извлечения работает следующим образом:
1. Каждый узел u проверяет каждую ультрафиолетовую ссылку, флажок которой bDeleted Ложен и  ультрафиолетовый
ультрафиолетовый > r, чтобы видеть, есть ли другой соседний w таким образом, что
> r, чтобы видеть, есть ли другой соседний w таким образом, что 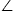 uwv
uwv 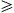 π/2 и ссылка vw существует. Если это имеет, то установленный флажок bDeleted ссылки, ультрафиолетовой, чтобы быть Истинным.
π/2 и ссылка vw существует. Если это имеет, то установленный флажок bDeleted ссылки, ультрафиолетовой, чтобы быть Истинным.
2. Все края, флажок которых bDeleted является Ложной формой заключительная структура.
В остатке от раздела мы показываем тому своему алгоритму, действительно заканчивает и производит плоскую структуру.
Мы сначала показываем этому, заключительная структура - действительно связанный плоский граф. Прежде всего, если оригинальный граф коммуникации будет связанным плоским графом, то наш алгоритм не будет добавлять виртуальных ссылок. Заключительная структура - только оригинальный граф коммуникации. Если алгоритм заканчивается с двумя пересеченными ссылками, говорить xy и ультрафиолетовый, то согласно доказательству Аннотации 1, мы знаем, что это пересечение будет обнаружено по крайней мере двумя из этих четырех узлов x, y, u, и v (в нашем доказательстве, мы показываем этому, u и y обнаружат пересечение, предполагая, что 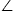 xuy - наибольший угол среди четырехугольника xuyv). Мы также показывали тому из узлов, решит добавить виртуальные ссылки (узлы u, и x добавит виртуальную ссылку ux в нашем предположении). Таким образом ссылка xy будет удалена в фазе Извлечения согласно нашему алгоритму. Таким образом, если алгоритм заканчивается, нет никаких пересеченных ссылок. Очевидно, что заключительная структура связана, если оригинальный граф коммуникации связан с тех пор, каждый раз когда мы решаем удалить ссылку, которая вызывает пересечение, мы уже добавили некоторые виртуальные ссылки (в случае необходимости), чтобы сформировать путь, подключающий две конечных точки удаленной ссылки. Кроме того, заключительная структура связана, так как мы удаляем край ультрафиолетовый iff, у нас есть подводные ссылки, и wv существуют (хотя любой из них мог быть виртуальной ссылкой).
xuy - наибольший угол среди четырехугольника xuyv). Мы также показывали тому из узлов, решит добавить виртуальные ссылки (узлы u, и x добавит виртуальную ссылку ux в нашем предположении). Таким образом ссылка xy будет удалена в фазе Извлечения согласно нашему алгоритму. Таким образом, если алгоритм заканчивается, нет никаких пересеченных ссылок. Очевидно, что заключительная структура связана, если оригинальный граф коммуникации связан с тех пор, каждый раз когда мы решаем удалить ссылку, которая вызывает пересечение, мы уже добавили некоторые виртуальные ссылки (в случае необходимости), чтобы сформировать путь, подключающий две конечных точки удаленной ссылки. Кроме того, заключительная структура связана, так как мы удаляем край ультрафиолетовый iff, у нас есть подводные ссылки, и wv существуют (хотя любой из них мог быть виртуальной ссылкой).
Мы тогда показываем тому своему алгоритму, действительно заканчивается. Заметьте, что, хотя мы делим свой алгоритм ко многим фазам, мы не должны строго следовать за этими фазами, то есть, различные узлы могут быть в различных фазах, и некоторый узел может возвратиться к некоторой более ранней фазе когда необходимо. Например, Виртуальная ссылка, Добавляющая фазу и Фазу Извлечения, может быть чередована.
Мы показываем этому, полная длина края структуры уменьшена всякий раз, когда мы обрабатываем пересеченную пару ссылок. Снова, предположите, что пересеченные ссылки xy и ультрафиолетовый обработаны. Подобный доказательству Аннотации 1, мы знаем, что у удаленной ссылки (край xy в нашем доказательстве) есть длина, большая чем возможно добавленная виртуальная ссылка (икс-единица края в нашем доказательстве). Заметьте, что, когда мы удаляем ссылку, возможно, что мы не должны добавить виртуальную ссылку (когда икс-единица уже - фактическая ссылка). С тех пор есть при большинстве ссылок n2/2 в сети n-узла, число связанных графов - также конечное число. Таким образом, наш алгоритм, как гарантируют, закончится.
После того, как плоская структура создана, мы тогда применяем некоторых ранее развитые протоколы маршрутизации на вершину этой структуры. Для законченности мы рассматриваем некоторых ограниченные протоколы маршрутизации, которые полагаются на плоскую структуру.
Правое правило - долго известный метод для того, чтобы пересечь граф (на аналогии со следующим за правой стеной в лабиринте). И это использовалось в некотором радио, направляющем протоколы [4], [23], [9] и [8]. Правило заявляет, что, достигая узла x от узла y, следующий пересеченный край является следующим последовательно против часовой стрелки о x от края xy. В примере, которому показывают в рис. 4, x отправит пакет z после правого правила, пересекая лицо P. Известно, что правое правило пересекает интерьер закрытой многоугольной области (лицо) в по часовой стрелке заказе края. И это пересекает внешнюю область в против часовой стрелки заказе края. Вообще, правое правило применено в плоских графах (в котором никакие края не пересекают друг друга). В [8] эвристическое без пересечений дано, чтобы иметь дело со случаем, где края пересекаются.
Рис. 4. Иллюстрация лица, направляющего алгоритм.
Применяя правое правило в плоских графах, протокол маршрутизации под названием Маршрутизация Лица предложен [11] (в газете, которую они называют Компасом алгоритма, Направляющим II). Мы рассматриваем плоский Г графа. Узлы и края Г графа делят Евклидов самолет в непрерывные области, названные лицами Г. Главная идея маршрутизации лица состоит в том, чтобы идти по лицам, которые пересечены линейным сегментом С-между источником s и адресатом t. В каждом лице это использует правое правило исследовать границы. Продвигающийся вокруг лица, алгоритм отслеживает пункты, где он пересекает линию С-. Полностью окружив лицо, алгоритм возвращается к одному из этих пересечений, лежащих самый близкий к t, где это продолжается, исследуя следующее лицо ближе к t. Рис. 4 приводит пример. См. [11] и [13] для детализированных алгоритмов. Они также доказали, что лицо, направляющее алгоритм, гарантирует, что достигло адресата t после пересечения в большинстве O (n) края, где n - число узлов.
Хотя маршрутизация лица заканчивается в линейное время, это не удовлетворительно, так как уже очень простой алгоритм наводнения закончит в O (n) шаги. Тогда в [13], Kuhn и др. предложил новый метод под названием Адаптивное Лицо, Направляющее (АФРИКАНСКИЙ), в котором, ограниченные области поиска используются, чтобы избежать исследовать полную границу лиц. Идея следующие. Исследование лиц ограничено области эллипса. Размер эллипса установлен в первоначальную смету оптимальной длины пути. Если маршрутизация лица не в состоянии достигнуть адресата (когда она достигает эллипса, она должна возвратиться), алгоритм перезапустит с эллипсом ограничения удвоенного размера. Они доказали, что алгоритм наконец найдет путь к t, если s и t будут связаны. Также число шагов АФРИКАНСКИХ ограничено O (c2 (p *)), где p* - оптимальный путь, и c (p *) является стоимостью того пути. В их доказательстве они предполагали, что граф диска модуля - цивилизованный граф. Наконец они дают плотное, ниже связанное, показывая, что у любого ограниченного геометрического алгоритма маршрутизации есть O стоимости худшего случая (c2 (p *)).
Недавно, Kuhn и др. [14] расширяет Адаптивную Маршрутизацию Лица на алгоритм маршрутизации под названием Другое Адаптивное Лицо, Направляющее (OAFR). Вместо того, чтобы измениться на следующее лицо в "лучшем" пересечении границы лица с С-, OAFR возвращается к граничной точке, самой близкой к адресату. Они доказали, что стоимость OAFR также ограничена O (c2 (p *)), который, асимптотически оптимально.
Жадная маршрутизация использовалась в раннем протоколе маршрутизации для беспроводных сетей. Однако, это просто создать простой пример, чтобы показать тому жадному алгоритму, не будет преуспевать, чтобы достигнуть адресата, но падения в местный минимум, узел без любых "лучших" соседей. Тогда естественный подход, чтобы улучшить потенциал жадной маршрутизации практически должен к объединению жадной маршрутизации и маршрутизации лица (или правое правило), чтобы возвратить маршрутизацию после того, как простая жадная маршрутизация терпит неудачу в местном минимуме. Много беспроводных протоколов использовали этот подход [4], [9], [14], [12], [23] и [25].
Жадный Периметр Не имеющая гражданства Маршрутизация (GPRS) [8] и [9] использование RNG или СТРОИТЕЛЬНОЕ СТЕКЛО как плоская топология маршрутизации, затем комбинирует жадное и правое правило отправить пакеты в сети. Это работает следующим образом. Когда узел получает пакет режима жадности, он ищет на своей соседней таблице соседа, который ближе к адресату t. Если будет один, то это отправит это тому соседу. Когда никакой сосед не ближе, узел отмечает пакет в режим периметра. GPSR вперед пакеты режима периметра, используя простое плоское пересечение графа (правое правило). Когда пакет вводит режим периметра, отчеты GPSR в пакете Долгоиграющая пластинка местоположения. Тогда получая пакет режима периметра, GPSR сначала сравнит это с отправлением местоположения узла. GPRS возвращается, пакет к жадному режиму расстояния от посылаемого узла до t - меньше чем это от Долгоиграющей пластинки до t. Для более подробного, пожалуйста обратитесь к [9] и [8]. GPRS может гарантировать поставку пакетов, когда основная сетевая топология - плоский граф.
Недавно, Kuhn и др. [14] предложил новый алгоритм, чтобы объединить жадную маршрутизацию с их Другим Адаптивным Лицом, Направляющим (OAFR). Они назвали новый метод Жадным Другим Адаптивным Лицом, Направляющим (GOAFR). Идея подобна GPSR. Когда жадные падения метода местного минимума, GOAFR использует OAFR, чтобы возвратить маршрутизацию. То же самое что касается АФРИКАНСКОГО, они доказали, что стоимость GOAFR ограничена O (c2 (p *)), который, асимптотически оптимально. Кроме того, они показывают этому, алгоритм - также средний случай, эффективный через обширные моделирования. В [14], авторы показывали моделированиям множества лица, направляющего алгоритмы и их комбинации с жадным подходом. Заметьте, что в отличие от GPSR, делая маршрутизацию лица в GOAFR, это не возвращается к жадному методу, пока OAFR полностью не заканчивает исследование лица. Это может затронуть эффективность маршрутизации. В [12], Kuhn и др. использует “раннее отступление” методика, чтобы возвратиться к жадной маршрутизации как можно скорее. Новый алгоритм называют GOAFR +. Это использует два счетчика p и q, чтобы отследить то, сколько из узлов, посещаемых во время текущего лица, направляющего фазу, расположены ближе (посчитанный p) и сколько не ближе (посчитанный q) адресату чем отправная точка текущего лица, направляющего фазу. Когда определенное условие отступления держится, GOAFR + непосредственно снижает скорость передачи данных к жадному режиму. Эта модификация делает очевидное усовершенствование для средней работы случая. Их теоретический анализ также доказывает, что GOAFR + асимптотически оптимален в худшем случае.
Мы провели обширные моделирования, чтобы изучить работу нашего метода по сравнению с предыдущим методом, предложенным в [1]. Мы сравниваем их и в терминах работы конструкции структуры и в терминах работы маршрутизации. Мы беспорядочно помещаем 500 узлов в квадрат с побочной длиной, изменяющейся от 7 до 15, и диапазон передачи каждого узла установлен к одному модулю. Прежде всего, мы хотим знать сколько сообщений, используемых этими двумя методами соответственно. Рис. 5 иллюстрирует quasi-UDG граф с 100 узлами в квадратной области 7. Рис. 6 (a) и (b) показывает виртуальным краям, добавленным во время процесса priori искусством и нашим методом. Рис. 6 (c) и (d) показывает заключительной топологии, произведенной этими двумя методами.
Рис. 5. Граф диска квазимодуля.
.jpg)
Рис. 6. (a) и (b): Виртуальные края, добавленные априорным искусством и нашим методом; (c) и (d): заключительная структура создана этими двумя методами. (a), (c) Priori искусство, (b), (d) наш метод.
Наш показ моделирований, что наш метод использует значительно меньше сообщений чем метод Barriére и др. [1] для плотных сетей. Используемые сообщения подобны для редких сетей. Подобное наблюдение держится для числа виртуальных ссылок созданный: наш метод создает значительно меньше виртуальных ссылок для плотных графов. См. рис. 7.
Рис. 7. Сравнение нашего метода с предыдущим методом. (a) Виртуальные края добавил и (b) используемые сообщения.
Заметьте, что, структура, которая может быть создана с меньшим количеством сообщений, не подразумевает, что работа маршрутизации, основанная на ней, лучше чем другая структура. Мы продолжаем изучать действия маршрутизации структур, созданных нашим методом и методом Barriére и др. [1]. Мы проверяем Жадное лицо, направляющее метод на структурах, созданных обоими методами (данный те же самые оригинальные графы коммуникации). Удивительно, мы нашли, что действия маршрутизации, основанные на этих двух структурах, являются почти тем же самым. См. рис. 8 для иллюстрации. Мы измерили и средние перелеты маршрута и средние длины маршрута. Заметьте, что, если маршрут использует созданную виртуальную ссылку, мы должны измерить перелеты и длины фактического пути, сохраненного в конечных точках, чтобы подключить их.
Рис. 8. Сравнение нашего метода с предыдущим методом. (a) Среднее число направляют перелеты и (b) среднюю длину маршрута.
Мы считаем беспроводную специальную сеть составленной из ряда беспроводных узлов распределенный в двух размерных самолетах. Несколько протоколов были развиты, чтобы выполнить маршрутизацию в специальных беспроводных сетях, основанных на позициях мобильных хостов. Типичное предположение в этих протоколах - то, что всем беспроводным узлам смоделировал однородные области передачи диск модуля, сосредоточенный в каждом беспроводном узле. Однако, все эти протоколы, вероятно, потерпят неудачу, если области передачи мобильных хостов не будут дисками модуля из-за естественных или искусственных препятствий или погодных условий. В этой газете мы описываем здравый протокол маршрутизации, который терпит примерно до 40 % изменения в диапазонах передачи мобильных хостов. Более точно, наш протокол гарантирует поставку сообщения в связанной специальной сети всякий раз, когда отношение максимального диапазона передачи к минимальному диапазону передачи самое большее![]() . Наш протокол сохранил стоимость коммуникации, не теряя действия по сравнению с предыдущим методом, который может терпеть то же самое различие передачи. Наши моделирования показывали тому нашему протоколу, выигрывает у предыдущего метода для плотных сетей значительно: это использует намного меньше сообщений и создает намного меньше виртуальных ссылок, в то время как действия маршрутизации нашего метода - почти то же самое как предыдущий метод.
. Наш протокол сохранил стоимость коммуникации, не теряя действия по сравнению с предыдущим методом, который может терпеть то же самое различие передачи. Наши моделирования показывали тому нашему протоколу, выигрывает у предыдущего метода для плотных сетей значительно: это использует намного меньше сообщений и создает намного меньше виртуальных ссылок, в то время как действия маршрутизации нашего метода - почти то же самое как предыдущий метод. ![]()
[1] L. Barrire, P. Fraigniaud, L. Narayanan, Здравая основанная на позиции маршрутизация в беспроводных специальных сетях с непостоянными диапазонами передачи, в: Слушания 5-ого Международного Симпозиума относительно Дискретных Алгоритмов и Методов для мобильных вычислений и Связи, 2001, стр 19–27.
[2] S. Basagni, я. Chlamtac, V.R. Syrotiuk, B.A. Лесничий, расстояние, направляющее алгоритм эффекта для подвижности (мечта), в: Слушания ACM/IEEE MobiCom ’98, 1998.
[3] P. Bose, P. Morin, Онлайн направляющий в триангуляциях, в: Слушания 10-ого Ежегодного Международного Симпозиума по Алгоритмам и Вычислению АЙЗЕК, 1999.
[4] P. Bose, P. Morin, я. Stojmenovic и J. Urrutia, Направляющий с гарантируемой поставкой в специальных беспроводных сетях, Беспроводных Сетях 7 (2001) (6), стр 609–616. Резюме-INSPEC | Резюме-Compendex | $Order Документ | Полный Текст через CrossRef
[5] K.R. Габриэль и R.R. Sokal, новый статистический подход к географическому анализу изменения, Систематическая Зоология 18 (1969), стр 259–278.
[6] D.B. Johnson и D.A. Maltz, Динамическая исходная маршрутизация в специальных беспроводных сетях. В: T. Imielinski и H.F. Korth, Редакторы, издание Мобильных вычислений 353, Kluwer Академические Издатели, Бостон (1996).
[7] B. Karp, H.T. Kung, Gpsr: жадный периметр не имеющая гражданства маршрутизация для беспроводных сетей, в: ACM/IEEE Международная Конференция по Мобильным вычислениям и Организации сети, 2000.
[8] B. Karp. Географическая Маршрутизация для Беспроводных Сетей, диссертации, Университета Гарварда, 2000.
[9] B. Karp, H.T. Kung, Gpsr: жадный периметр не имеющая гражданства маршрутизация для беспроводных сетей, в: Слушания Международной Конференции ACM/IEEE по Мобильным вычислениям и Передающий (MobiCom), 2000.
[10] Y.-B. Ko, N.H. Vaidya, Используя информацию местоположения, чтобы улучшить маршрутизацию в специальных сетях, Техническом сообщении, Отделе Информатики, Техас Университет A&M, 1997.
[11] E. Kranakis, H. Singh, J. Urrutia. Маршрутизация компаса на геометрических сетях, в: Слушания 11-ой канадской Конференции по Вычислительной Геометрии, 1999, стр 51–54.
[12] F. Kuhn, R. Wattenhofer, Y. Zhang, A. Zollinger. Геометрическая маршрутизация для данного случая: из теории и практики, в: Слушания 22-ого Международного Симпозиума ACM по Принципам Распределенного Вычисления (PODC), 2003.
[13] F. Kuhn, R. Wattenhofer, и A. Zollinger, Асимптотически оптимальная геометрическая мобильная маршрутизация для данного случая, в: Слушания 6-ого Международного Симпозиума относительно Дискретных Алгоритмов и Методов для Мобильных вычислений и Связи (DIALM), 2002.
[14] F. Kuhn, R. Wattenhofer, A. Zollinger, оптимальный Худший случай и средний случай эффективная геометрическая маршрутизация для данного случая, в: Слушания 4-ого Международного Симпозиума ACM по Мобильной Организации сети Для данного случая и Вычислению (MobiHoc), 2003.
[15] X.-Y. Литий, Г. Calinescu, P.-J. Бледная, Распределенная конструкция плоского гаечного ключа и направляющий для специальных беспроводных сетей, в: 21-ая Ежегодная Объединенная Конференция ИИЭРа Компьютер и Общества Связи (INFOCOM), издание 3, 2002.
[16] S. Murthy и J. Garcia-Luna-Aceves, эффективный протокол маршрутизации для беспроводных сетей, Мобильных Сетей и Приложений 1 (1996) (2) Специальный выпуск при Маршрутизации в Сетях Мобильной коммуникации.
[17] V. Парк, М. Corson, очень адаптивный распределенный алгоритм маршрутизации для мобильных беспроводных сетей, в: ИИЭР Infocom, 1997.
[18] C. Perkins, Для данного случая по требованию векторная маршрутизация расстояния, в: MILCOM ’97, ноябрь 1997.
[19] C. Perkins, P. Bhagwat, Очень динамическая упорядоченная адресатом маршрутизация вектора расстояния, в: Слушания ACM SIGCOMM, октябрь 1994.
[20] S. Ramanathan и М. Steenstrup, обзор маршрутизации методик для сетей мобильной коммуникации, Мобильных Сетей и Приложений 1 (1996) (2), стр 89–104. Резюме-Compendex | $Order Документ | Полный Текст через CrossRef
[21] E. Royer и C. Toh, обзор текущих протоколов маршрутизации для мобильных беспроводных сетей для данного случая, Связь Персонала ИИЭРа 6 (1999) (2), стр 46–55. Резюме-INSPEC | $Order Документ | Полный Текст через CrossRef
[22] P. Sinha, R. Sivakumar и V. Bharghavan, Кедр: основное извлечение распределило специальный алгоритм маршрутизации, ИИЭР Журнал на Отобранных Областях в Связи 17 (1999) (8), стр 1454–1465.
[23] Я. Stojmenovic и X. Lin, гибрид Без петель single-path/flooding маршрутизация алгоритмов с гарантируемой поставкой для беспроводных сетей, ИИЭР Сделки на Параллельных и Распределенных Системах 12 (2001) (10).
[24] G.T. Toussaint, относительный граф соседства конечного плоского набора, Распознавание образов 12 (1980) (4), стр 261–268. Резюме | Полный Текст + Ссылки | PDF (469 K) | MathSciNet
[25] Y. Yu, R. Govindan, D. Estrin, Географический и энергия осведомленная маршрутизация: рекурсивный протокол распространения данных для беспроводных сетей датчика, Техническое сообщение, Отдел Информатики UCLA Техническое Сообщение UCLA/CSD-TR-01-0023, 2001. ![]()
.jpg) |
Kousha Moaveninejad принял Бакалавра в Компьютере Мягкая Разработка от Университета Sharif Технологии, Тегерана/Ирана, в 1997. Он присоединился к Отделу Информатики Института Иллинойса Технологии в 2000, как студент M.S. и получил степень Хозяина в 2002. Он тогда продолжал свое исследование как аспирант в Институте Иллинойса Технологии, и его текущие исследовательские интересы включают беспроводные сети для данного случая, вычислительную геометрию, дизайн алгоритма, и мобильные вычисления. |
.jpg) |
Песня Жировика-Zhan приняла БАКАЛАВРА НАУК и MS от Наньцзинского Университета Науки и техники в 1997 и 2000. Он в настоящее время - кандидат доктора философии Информатики в Институте Иллинойса Технологии. Он работал в промышленности телекоммуникации с 1997 до 2001 как программный системный проектировщик и руководитель группы. Его текущий исследовательский интерес, главным образом сосредотачиваются на сетевом протоколе и дизайне алгоритма, особенно в беспроводных сетях, сетях датчика и Одноранговых сетях. Он - студенческий член ИИЭРа. |
.jpg) |
Литий Сянцзяна-яна был Доцентом Информатики в Институте Иллинойса Технологии с 2000. Он держит MS (2000) и доктор философии (2001) степень в Информатике от Университета Иллинойса в Urbana-равнине. Он получил свою степень Бакалавра в степени Информатики и Бакалавра в Деловом Управлении от Университета Tsinghua, P.R. Китай в 1995. Его исследовательские интересы охватывают вычислительную геометрию, беспроводные специальные сети, теорию игры, шифрование и сетевую безопасность. Он - гость-редактор для специального выпуска MONET на несовместном вычислении в беспроводных сетях. Он - Член ACM, ИИЭРа, и Общества Коммуникации ИИЭРа. |
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Том 3, Проблема 5, сентябрь 2005, Страницы 546-559 Передача данных и Управление Топологии в Специальных Сетях | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Авторское право © 2005 Elsevier B.V. Все права защищены. ScienceDirect® - регистрированная торговая марка Elsevier B.V. |